一、录取名单
| 序号 |
姓名 |
学校(详细至学院) |
| 1 |
Denis Mukama |
东北师范大学数学与统计学院 |
| 2 |
柏延松 |
吉林大学数学学院 |
| 3 |
蔡 猛 |
中南大学数学与统计学院 |
| 4 |
陈 星 |
东北师范大学数学与统计学院 |
| 5 |
陈昊天 |
吉林大学数学学院 |
| 6 |
程梦雨 |
大连理工大学数学科学学院 |
| 7 |
程秀俊 |
浙江理工大学理学院 |
| 8 |
崔媛萍 |
东北师范大学数学与统计学院 |
| 9 |
代新杰 |
湘潭大学数学与计算科学学院 |
| 10 |
邓定文 |
南昌航空大学数学与信息科学学院 |
| 11 |
邓寿年 |
安徽工程大学数理学院 |
| 12 |
葛美宝 |
上海财经大学数学学院 |
| 13 |
耿一丹 |
哈尔滨工业大学数学学院 |
| 14 |
郭 平 |
大连理工大学数学科学学院 |
| 15 |
郭雪婷 |
苏州大学数学科学学院 |
| 16 |
何 婕 |
上海师范大学数理学院 |
| 17 |
柯雨霏 |
上海财经大学数学学院 |
| 18 |
李贺宇 |
吉林大学 |
| 19 |
李精玉 |
吉林大学数学研究所 |
| 20 |
李晓翠 |
北京化工大学数理学院 |
| 21 |
刘 微 |
吉林大学数学学院 |
| 22 |
刘 欣 |
大连理工大学数学科学学院 |
| 23 |
刘鑫禹 |
东北师范大学数学与统计学院 |
| 24 |
刘 艺 |
东北师范大学数学与统计学院 |
| 25 |
刘玉芬 |
东南大学数学学院 |
| 26 |
吕阳阳 |
吉林大学数学学院 |
| 26 |
马宇婷 |
东北师范大学数学与统计学院 |
| 28 |
曲世铎 |
吉林大学数学学院 |
| 29 |
宋国婷 |
东北师范大学数学与统计学院 |
| 30 |
唐 晓 |
南方科技大学数学系 |
| 31 |
唐志强 |
吉林大学数学学院 |
| 32 |
王家宝 |
吉林大学数学学院 |
| 33 |
王贵黔 |
上海师范大学数理学院 |
| 34 |
王梦超 |
中南大学数学与统计学院 |
| 35 |
熊美馨 |
华中科技大学数学与统计学院 |
| 36 |
陈柳红 |
华中科技大学数学与统计学院 |
| 37 |
尤 波 |
西安交通大学数学与统计学院 |
| 38 |
张 红 |
宁夏大学数学统计学院 |
| 39 |
张静静 |
华东交通大学理学院 |
| 40 |
张 琪 |
沈阳工业大学理学院 |
| 41 |
张宇航 |
哈尔滨工业大学数学学院 |
| 42 |
赵浩竹 |
吉林大学数学学院 |
| 43 |
赵 昕 |
南京理工大学理学院 |
| 44 |
朱佳楠 |
吉林大学数学院 |
| 45 |
朱美瑾 |
东南大学数学学院 |
二、课程安排
2019年随机计算暑期短课程-8月

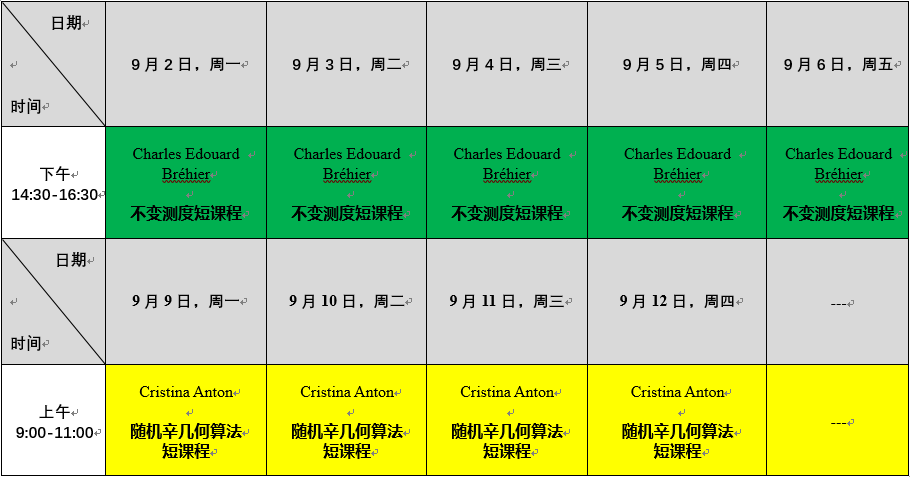
2019年随机计算暑期短课程-9月
三、预备知识及参考教材
2019年“随机微分方程计算方法及其数学理论”暑期短课程包括4门课程,具体如下:
1、课程名称:大偏差短课程(Large Deviations Principle)
授课老师:Xia Chen(University of Tennessee, USA)
预备知识:The prerequisites for the audience is the first probability course in
graduate level.
参考教材:
1. Large deviations---Techniques and application By Amir Dembo and Ofer Zeitouni
2.课程名称:SPDEs及数值方法短课程(Numerical Methods of SPDE)
授课老师:Gabriel J. Lord(Heriot-Watt University, United Kingdom)
预备知识:无
参考教材:无
3.课程名称:不变测度短课程(Numerical Approximation of Invariant Distributions for SPDEs)
授课老师:Charles Edouard Bréhier(Claude Bernard University Lyon 1, France)
预备知识:numerical analysis and probability. If possible: Brownian Motion and Stochastic Differential Equations.
参考教材:无
4.课程名称:随机辛几何算法短课程(Symplectic Methods of Stochastic Hamiltonian Systems)
授课老师:Cristina Anton(MacEwan University, Canada)
预备知识:The students should have some basic knowledge about stochastic differential equations, stochastic integration,numerical schemes, and some knowledge about probability and stochastic processes (e.g. properties of expectations, convergences)
参考教材:无
四、学员待遇
中心为非长春本地的正式学员提供免费住宿,为考核优秀的学员提供一定的生活补助,中心还为正式学员提供讲义、互联网、自习室等辅助学习条件。
