The First International Workshop on
China-Russia Mathematics
January 10th, 2021
Heilongjiang University, Harbin, China
Organizers:
School of Mathematical Science, Heilongjiang University
China-Russia College, Heilongjiang University
China-Russia Mathematical Center at Peking university
Tianyuan Mathematical Center in Northeast China
Financial support:
Heilongjiang University
National Natural Science Foundation of China
Scientific Committee:
Jiping Zhang (Peking University) ……
Sergey I. Kabanikhin (Siberian Branch, RAS) ……
Organizing Committee:
Xiaomin Tang (Professor, Heilongjiang University, China)
Xujie Jia (Professor, Heilongjiang University, China)
Jinliang Wang (Professor, Heilongjiang University, China)
Lei Zhang (Professor, Heilongjiang University, China)
Ran Zhang (Professor, Jilin University, China)
Conference Venue:
All the talks will be held online using Zoom Meeting platform.
Conference Schedule:
Jan. 10th (Sunday) (Beijing time):
The opening ceremony; Full-day meeting, The closing ceremony.
Contact Information:
Registration and Abstract Deadlines: Pre-registration: Dec. 31st, 2020, Abstracts: Jan. 5, 2021.
Participants, please contact with:
Jinliang Wang, Email: jinliangwang@hlju.edu.cn Tel: +86 18945077863
Lei Zhang, Email: zhanglei@hlju.edu.cn Tel: +86 18686658960
Workshop Introduction
The First International Workshop on China-Russia Mathematics will be held online from January 10th, 2021, and hosted by Heilongjiang University. This workshop aims to bring together experts working in mathematics to present their latest research findings, share innovative ideas, identify challenges, and promote international collaborations in Algebra, Geometry, Differential equations, Dynamical systems, Inverse problems, and their real-world applications. All the talks will be held online using the Zoom Meeting platform. This workshop gets great support from the Heilongjiang University, China-Russia Mathematical Center at Peking University, and Tianyuan Mathematical Center in Northeast China.
SCHEDULE
The First International Workshop on China-Russia
Mathematics
Time: Jan. 10th, 2021 (Beijing time)
Venue: All the talks will be held online using Zoom Meeting platform.
Session I
---------------------------------------------------------------------------------------------------
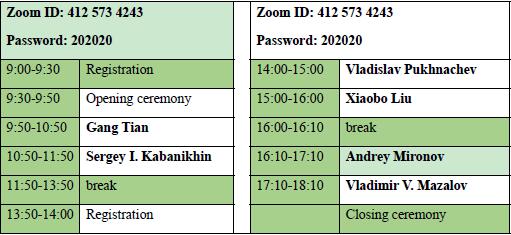
Jan. 10th, Morning (Beijing time) Jan. 10th, Afternoon (Beijing time)
Session II (A series of conferences are in preparation)
-----------------------------------------------------------------------------------------------------
TBA
Program
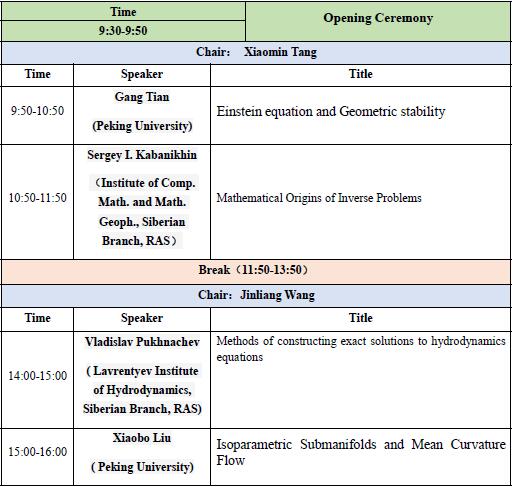
January 10th,2021 (Beijing time),Morning Session,Zoom ID: 412 573 4243, Password:202020
January 10,2021 (Beijing time),Afternoon Session,Zoom ID: 412 573 4243, Password:202020
Titles and abstracts
(in presentation order)
----------------------------------------------------------------------------------------
Einstein equation and Geometric stability
Gang Tian (田刚)
Peking University
This is an expository talk on existence of Kahler-Einstein metrics which are special solutions of the Einstein equation. This existence problem has been studied since 1950s and there were substantial progresses in last decade. I will discuss some of the progresses and some recent developments.
-----------------------------------------------------------------------------------------------------
Mathematical Origins of Inverse Problems
Sergey I. Kabanikhin(谢尔盖I.卡巴尼钦)
Institute of Computational Mathematics and Mathematical Geophysicss, Siberian
Branch, RAS
Inverse Problems is a very new scientific discipline connected with Mathematics,Applied Mathematics, Statistics, Physics and other Natural and Social Sciences. An inverse problem in science is the process of calculating from a set of observations the causal factors that produced them: calculating an image in X-ray computed tomography, source or medium properties reconstruction in acoustics and electrodynamics, or calculating the density of the Earth from measurements of its gravity field. It is the
inverse of a forward problem, which starts with the causes and then calculates the effects. Inverse problems are some of the most important mathematical problems in science and mathematics because they tell us about parameters that we cannot directly observe. They have wide application in system identification, optics, radar, acoustics, communication theory, signal processing, medical imaging, computer vision, geophysics, remote sensing, natural language processing, machine learning, nondestructive testing, and many other fields. A little more than seventy years of studying problems of this kind have shown that a great number of problems from various branches of classical mathematics (computational algebra, differential and integral equations, partial differential equations, functional analysis) can be classified as inverse or ill-posed, and they are among the most complicated ones (since they are unstable and usually nonlinear). We will discuss the connection between Inverse Problems and Algebra, Geometry, Calculus, Functional Analysis and Optimization.
-----------------------------------------------------------------------------------------------------
Methods of constructing exact solutions to hydrodynamics equations
Vladislav Pukhnachev (芙拉蒂丝拉夫. 普赫纳切夫)
Lavrentyev Institute of Hydrodynamics, Siberian Branch, RAS
(1) Basic hydrodynamic models and Lie groups admitted by them. Navier-Stokes and Euler equations. Gas dynamic equations. Porous medium equation. (2) Lagrangian coordinates. Motions with uniform deformation. Ellipsoids of Dirichlet and Ovsyannikov. (3) Method of differential constrains. Trkal solution to Navier-Stokes equations. Simple and double waves in gas dynamics. (4) Method of invariant subspaces.
Applications to problems of liquid and gas motion in porous medium. (5) Invariant solutions of free boundary problems. Spreading of viscous layer on rotating plane.
-----------------------------------------------------------------------------------------------------
Isoparametric Submanifolds and Mean Curvature Flow
Xiaobo Liu (刘小博)
Peking University
Ancient solutions are important in studying singularities of mean curvature flows(MCF). So far, most rigidity results about ancient solutions are modeled on shrinking spheres or spherical caps. In this talk, I will describe the behavior of MCF for a class of submanifolds, called isoparametric submanifolds, which have more complicated topological type. We can show that all such solutions are in fact ancient solutions, i.e.they exist for all time which goes to negative infinity. Similar results also hold for MCF of regular leaves of polar foliations in simply connected symmetric spaces with non-negative curvature. I will also describe our conjectures proposed together with Terng on rigidity of ancient solutions to MCF for hypersurfaces in spheres. These conjectures are closely related to Chern’s conjecture for minimal hypersurfaces in spheres. This talk is based on joint works with Chuu-Lian Terng and Marco Radeschi.
-----------------------------------------------------------------------------------------------------
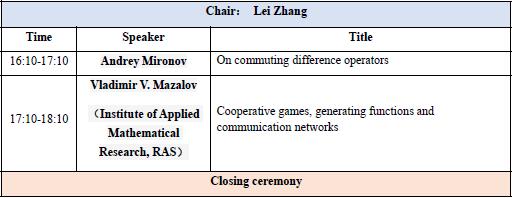
On commuting difference operators
Andrey Mironov(安德烈. 米洛诺夫)
Sobolev Institute of Mathematics, Siberian Branch, RAS
We consider one-point commuting difference operators of rank one. The coefficients of these operators depend on a functional parameter, shift operators being included only with positive degrees. We study these operators in the case of hyperelliptic spectral curve when the marked point coincides with the branch point. We construct examples of operators with polynomial and trigonometric coefficients. Moreover, difference operators with polynomial coefficients can be embedded in the differential ones with
polynomial coefficients. This construction provides a new way of constructing commutative subalgebras in the first Weyl algebra.
-----------------------------------------------------------------------------------------------------
Cooperative games, generating functions and communication networks
Vladimir V. Mazalov (弗拉基米尔. 马扎洛夫)
Institute of Applied Mathematical Research, KRC, RAS
The main problem in cooperative games is the distribution of total payoff. We show how generating functions can be used to find solutions in cooperative games. They can be used to calculate the Banzaf and Shapley-Shubik values in voting games. Recently, it has been shown that the methods of cooperative games can be effectively used in the analysis of communication graphs and social networks. Here we show how generating functions are used in games with restricted cooperation to calculate the Myerson value. Then we show their application in the problems of finding stable coalition structures in networks.
-----------------------------------------------------------------------------------------------------
The First International Workshop on China-Russia Mathematics
Heilongjiang University, January 10th, 2021
Speakers Information
-----------------------------------------------------------------------------------------------------
Gang Tian (田刚):国际著名数学家,中国科学院院士,北京大学讲席教授、北京国际数学研究中心主任。1994年获美国国家科学基金委员会第十九届沃特曼奖,1996年获美国数学会韦伯伦奖,1990年在世界数学家大会上作45分钟报告,2002年在世界数学家大会上作1小时大会报告。2001年当选为中国科学院院士,2004年当选为美国科学与艺术院院士,2018年当选为国际数学联盟执委会委员,2019年当选为中国数学会理事长。解决了一系列几何及数学物理中的重大问题,特别是在Kahler-Einstein度量研究中做了开创性工作。解决了Kahler-Einstein度量存在性这
个60年来悬而未决的世界数学难题。是Gromov-Witten不变量理论的奠基人之一。在高维规范场数学理论研究中也有杰出成就,对解决著名的庞加莱猜想也做出了重要贡献。
-----------------------------------------------------------------------------------------------------
Sergey I. Kabanikhin(谢尔盖I.卡巴尼钦): 俄罗斯科学院西伯利亚分院通讯院士。俄罗斯科学院西伯利亚分院计算数学和数学地球物理研究所(ICM&MG SB RAS)科学委员会主席,俄罗斯科学院西伯利亚分院主席团成员,俄罗斯科学院数学科学系主席团成员,俄罗斯科学院西伯利亚分院超级计算委员会主席,数学和信息学联合科学委员会副主席, 索伯列夫数学研究所科学委员会成员,俄罗斯国家科学院力学和数学系科学委员会成员。他的主要研究方向不适定问题的数值方法在地球物理,包括地震,电勘探,重力勘探,磁勘探;断层扫描;处理物理测量,数据解释等问题中的应用。主要研究成果:1、电动力学中求解反问题的数值方法的发展和验证。该结果被用于证明一种新的电勘探方法是正确的,该方法基于对不稳定电磁场的激发和测量。2、在条件稳定性估计的基础上,导出适用于不适定问题的梯度方法的强收敛速度的估计。这允许根据数据错误和条件稳定率引入新的停止规则。3、与I.V. Koptyug和K.T. Iskakov合作发展了拟线性抛物方程反问题算法的,这种算法被用于核磁共振成像。4、与M.A. Shishlenin 和N.S. Novikov合作研构造了盖尔范德-莱维坦方程和克莱恩方程的多维模拟的算法,这些方程被用于创建声学和弹性多维反问题的数值求解。5、构建由钻孔环境中的亚纳秒探针激发的电磁场模型,并开发用于解决确定宿主介质的电磁特性的反问题的算法。6、建立一种解决重建地震和海啸源的逆问题的方法(与A. Hasanoglu, I.G. Marinin, and O.I. Krivorotko合作)。这些结果为快速建模、分析和预测自然和人为灾害风险的数值算法和软件奠定了基础。7、发展了求解药物动力学反问题的理论和数值方法。Kabanikhin博士发表科学论文200余篇,出版10余部专著,是包括Inverse and Ill-Posed Problems等多个杂志的主编和编委。
-----------------------------------------------------------------------------------------------------
Vladislav Pukhnachev(芙拉蒂丝拉夫,普赫纳切夫): 俄罗斯科学院西伯利亚分院通讯院士。1961年莫斯科物理技术学院毕业,1974年获博士学位。1998年当选为俄罗斯科学院的通讯院士。世界著名的连续介质力学领域的知名专家。他的工作主要方向是连续力学的数学问题。考虑到化学反应的有限速率,他是第一个研究Chapman-Jouguet爆炸过程稳定性的人。获得的结果有助于了解自旋爆轰发生的条件。证明了Navier-Stokes方程的自由边界问题,特别是滚动波的Kapitza问题的第一个存在性和唯一性定理。他找到了解决这些问题的各种精确解决方案,证实了
带有自由边界的粘性流的近似模型,研究并开发了热毛细管对流和Marangoni边界层的理论。开发了拉格朗日坐标法来研究Stefan问题和Cauchy问题,用于退化滤波方程。提出了粘性流体中物体的自推进问题,并为其数值解开发了一种算法。对零重力下流体的动力学和传热进行了研究,旨在为空间技术创造科学基础。他是第一个研究结晶逆问题的人。热引力对流理论中模型的构造层次结构使得可以概述经典Oberbeck-Boussinesq方程的适用范围,并提供了一种在微尺度,弱力或快速变化的温度场中计算对流的有效方法。他是俄罗斯理论和应用力学国家委员会的成员。也是许多全俄和国际会议的组织委员会主席和成员。
-----------------------------------------------------------------------------------------------------
Xiaobo Liu (刘小博): 北京大学教授、博士生导师、北京国际数学研究中心副主任、北京大学数学研究所副所长。主要研究方向为微分几何、数学物理,主要研究领域集中在Gromov-Witten 不变量普适方程和Virasoro 猜想, 在Annals of Math,American Journal of Math等国际著名期刊上发表多篇高质量论文。2006年受邀在西班牙马德里召开的世界数学家大会上做特邀报告。
-----------------------------------------------------------------------------------------------------
Andrey Mironov(安德烈•米洛诺夫): 俄罗斯科学院西伯利亚分院首席研究员。2011年获数学物理博士学位。历任索伯列夫数学研究所助理研究员,研究院,首席研究员, 同时也是新西伯利亚国立大学几何与拓扑学系主任。2016年入选俄罗斯科学院教授。主要研究领域:微分几何,代数拓扑。在Inventiones Mathematicae、Advances in Mathematics 、Communications in Mathematical Physics, International Mathematics Research Notices 等杂志发表70 余篇研究论文。个人主页:http://www.math.nsc.ru/LBRT/d6/mironov/index.html。
-----------------------------------------------------------------------------------------------------
Vladimir V. Mazalov(弗拉基米尔•马扎洛夫): 俄罗斯科学院卡莱利亚研究中心应用数学研究所所长,教授。俄罗斯运筹学会现任主席。马扎洛夫教授在圣彼得堡国立大学获得数学控制论博士学位(1981年),在圣彼得堡国立大学获得康复学博士学位(1991年)。1980-98年在东西伯利亚赤塔自然资源研究所从事俄罗斯科学院资助的研究项目。目前在俄罗斯科学院卡莱利亚研究中心应用数学研究所工作,同时也是彼得罗扎沃茨克国立大学概率论系教授。主要研究方向:合作博弈论、网络博弈论、行为博弈论与运筹学。在网络、交通模型和行为生态学的建模和控
制等领域的研究成果影响深远。担任多个学术杂志(International Game Theory Review,Scientiae Mathematicae Japonicae, Journal of the Operations Research Society of China, Operations Research and Decisions)的副主编。
-----------------------------------------------------------------------------------------------------
黑龙江大学数学科学学院简介
黑龙江大学数学科学学院的前身是1958 年开始招生的数学系,是黑龙江大学更名时的七个系之一。至今,学院的本科教学、科研工作已有60 余年的悠久历史,已经培养本科生4000 余名,硕士研究生400 余名,他们中包括首届国家杰出青年基金获得者李建中教授,中科院百人计划研究员徐国良研究员等优秀人才。作为黑龙江省省级理科基础科学研究与人才培养基地,学院具有优良的教风、学风。
黑龙江大学数学科学学院现设有数学与应用数学、信息与计算科学、统计学三个本科专业,数学(2012 年)、统计学(2012 年)两个一级学科硕士科学学位授权点,应用统计硕士专业学位授权点。涵盖基础数学、应用数学与计算数学、运筹学与控制、统计学等二级学科。数学与应用数学专业、信息与计算科学专业为“十二五”黑龙江省普通高等学校重点本科专业。数学学院始终对教书育人和科学研究并重。1987 年在全国科学大会上,刘礼泉教授获得全国科学大会三等奖。1993 年刘德祥教授获得国家优秀教师称号。王路群教授、向新民教授、曹重光教授分别获得黑龙江省优秀教师称号,后多次获得省级教书育人标兵称号。目前学院共有教师73 人,其中专任教师66 人;教授11 人、副教授31 人;有博士学位的46 人。“十三五”期间专任教师队伍中有12 人(负责人)获国家自然科学基金项目资助,1 人入选黑龙江省教育厅新世纪优秀人才支持计划,1 人入选黑龙江省普通本科高等学校青年创新人才培养计划,2 人入选黑龙江大学学科青年学术骨干百人支持计划。
数学科学学院现拥有黑龙江省复杂系统理论与计算重点实验室,黑龙江大学大型科学计算重点实验室,黑龙江大学复杂系统分析与控制重点实验室。实验室能够进行高速网络互连和资源共享,为广大同学的学习和科技创新活动创造了良好的软硬件平台。
凭借扎实的本科教学和丰富的科研资源不断提升学生的专业素养。该院本科学生多次获得全国数学竞赛和数学建模竞赛一、二等奖,在中俄大学生数学竞赛中,该院学生多次获得大奖,特别是2013 年包揽了全部的最高奖项,为黑龙江大学数学科学学院赢得了很高的国际赞誉。数学科学学院的本科毕业生就业率始终在省内同类专业中名列前茅,近五年就业率均达到95%以上,其中约20%的毕业生继续攻读硕士学位,其他毕业生则进入到计算机、金融、教育、数据分析等热门就业行业中。多年来,我院毕业生得到社会及用人单位的肯定与好评。
黑龙江大学中俄学院简介
黑龙江大学中俄学院是国家级重点试点学院,隶属于黑龙江大学,是中华人民共和国黑龙江大学与俄罗斯新西伯利亚国立大学按照国际一流学院发展理念与模式、联合建立的以服务中俄战略协作伙伴关系为宗旨、以培养对俄战略性拔尖创新人才为目标的公办全日制学院,2011 年5 月13 日由黑龙江省教育厅批准成立,同年10 月,经国家教育体制改革领导小组批准成为全国首批17 所试点学院之一,同时也是所有试点学院中唯一一所具有鲜明中外合作办学特色的学院。目前,学院的前期改革建设工作已取得初步成效,获得了国务院、教育部等上级领导的关注和肯定,办学成绩写入中俄两国总理会谈纪要,得到中俄两国领导的认可。2012年4 月,学院获批自主招生权,步入全国90所自主招生院校行列,使黑龙江大学成为全国唯一一所拥有自主招生权的非985、211 高校。